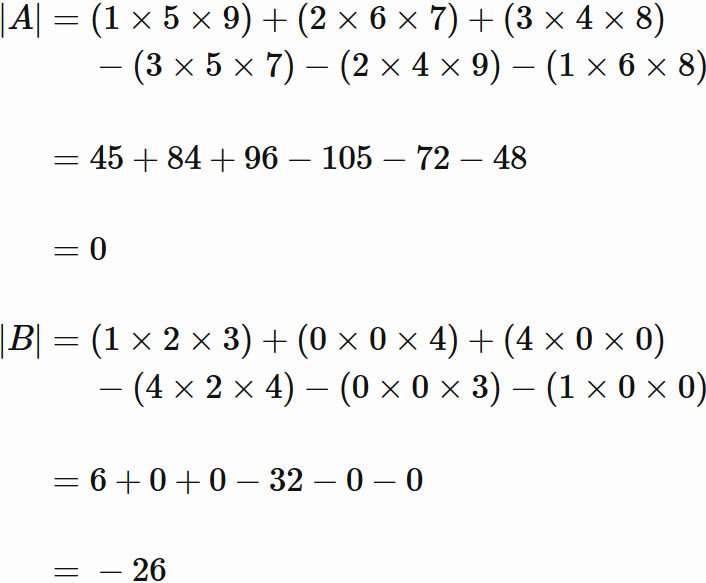3次の行列式
| 目次 | |
|---|---|
| - | $3\times 3$ の行列式 |
| - | 例題 |
| - | 計算機 |
| - | サラスの公式 |
| - | スカラー三重積 |
3次の行列式
$3$ 次の正方行列

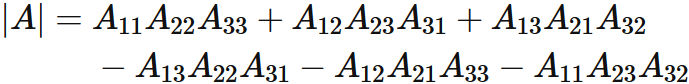
証明
列について余因子展開 を利用する(3次の余因子展開はこちらを参考)。 $|A|$ の行列式を $1$ 列について余因子展開すると、
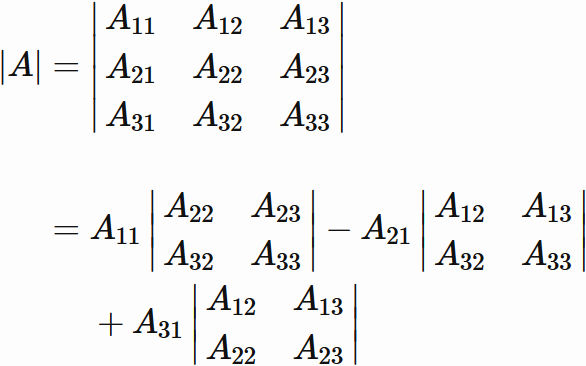 である。
それぞれの項に現れた 2 次の行列式を表すと、
である。
それぞれの項に現れた 2 次の行列式を表すと、
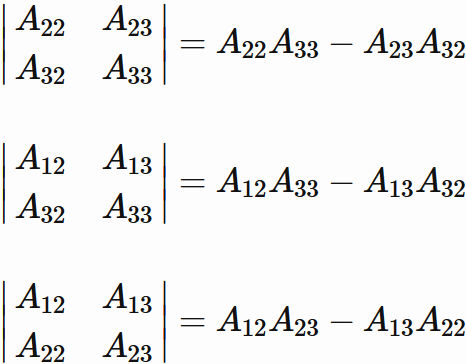 である。
これより
である。
これより
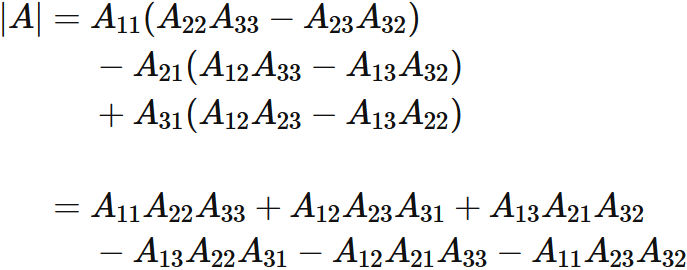 を得る。
を得る。
列について余因子展開 を利用する(3次の余因子展開はこちらを参考)。 $|A|$ の行列式を $1$ 列について余因子展開すると、
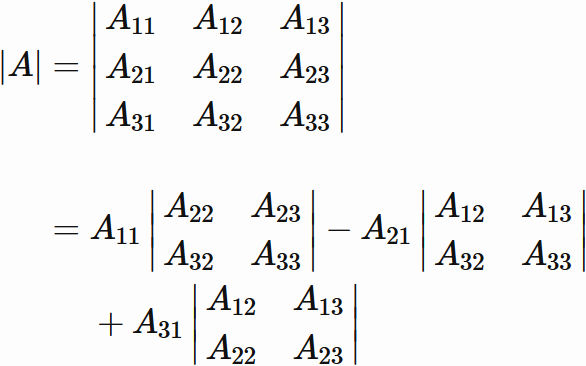
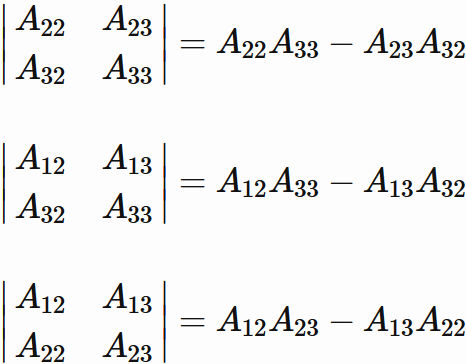
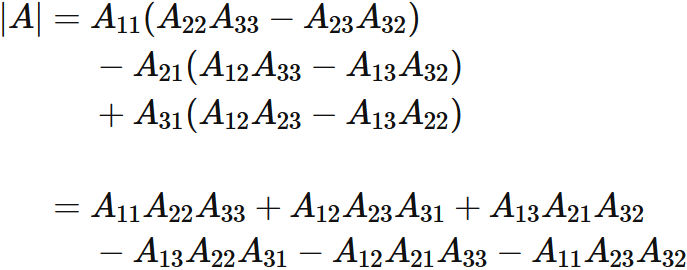
具体例
例題
3次の正方行列
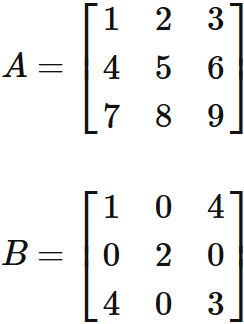
計算用入力フォーム
下記入力フォームに半角数字で値を入力し、「実行」ボタンを押してください。行列式の計算結果が表示されます。
サラスの公式
3次の行列式は2次の行列式と比較してやや複雑なので、
覚えておくための公式がある。
$3 \times 3$ の行列 $A$ の左上から右下に向けて $5$ 本の線を引く。
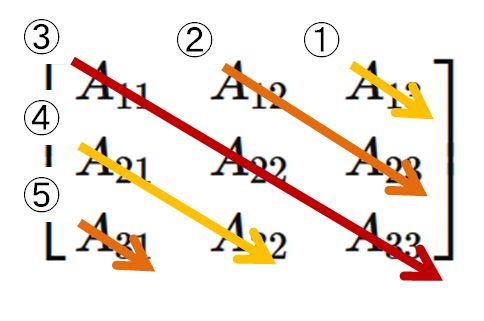
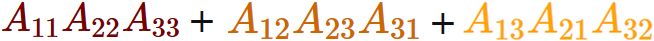
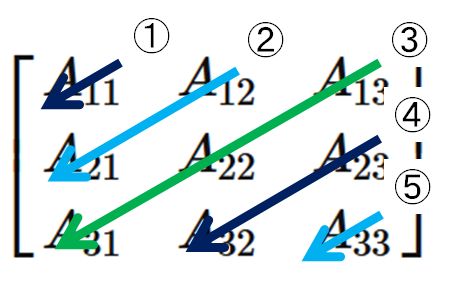
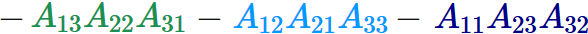
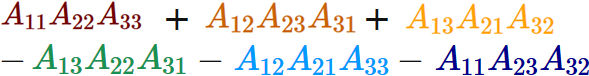
このように $3$ 次の行列式は、 左上から右下に向けて線を引いて得られる項を足し合わせ、 右上から左下に向けて線を引いて得られる項を引くと得られる。 この覚え方をサラスの公式という。
サラスの公式はそれほど覚えやすい公式ではないが、 同じような考え方で $2$ 次の行列式も得られるので重宝されることがある。 ただし、$4$ 次以降の行列式には適用できない。
スカラー三重積
$3$ 次元ベクトル $\mathbf{a}$ と $\mathbf{b}$ と $\mathbf{c}$ のスカラー三重積は、
それぞれを列ベクトルに持つ $3$ 次の行列式に等しい。
すなわち、
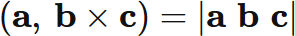
証明: スカラー三重積に等しい