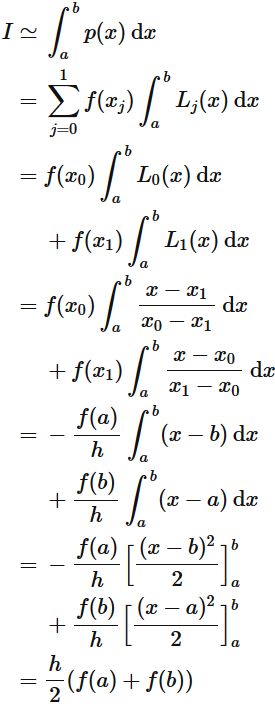
台形公式とシンプソン公式
台形公式
積分
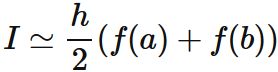
解説
積分
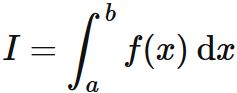 の被積分関数 $f(x)$ を $2$ 点
の被積分関数 $f(x)$ を $2$ 点
 $$
\tag{1}
$$
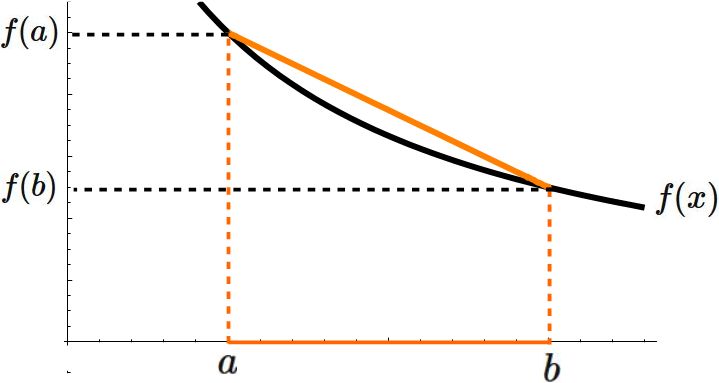
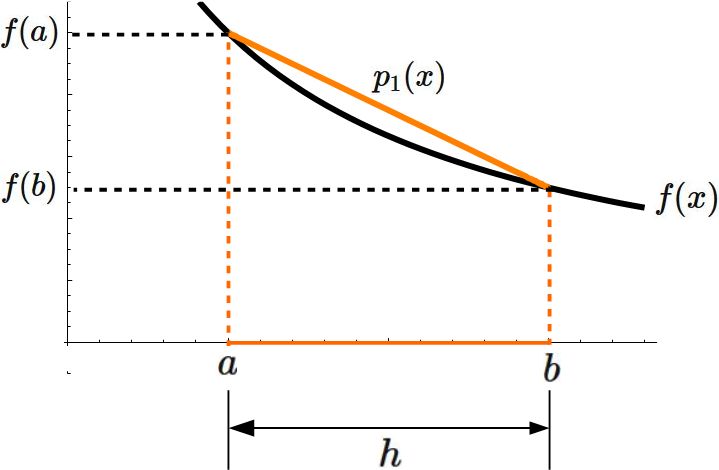
を通る直線で近似し、その積分によって $I$ の近似値を与える公式を台形公式という。
直線と積分区間によって囲まれた領域が台形になることにちなんで台形公式という名前が付いている(下図)。
$$
\tag{1}
$$
を通る直線で近似し、その積分によって $I$ の近似値を与える公式を台形公式という。
直線と積分区間によって囲まれた領域が台形になることにちなんで台形公式という名前が付いている(下図)。
 台形公式を求める。
$2$ 点 $(1)$ を通る直線を $p_{1}(x)$ とすると、
台形公式を求める。
$2$ 点 $(1)$ を通る直線を $p_{1}(x)$ とすると、
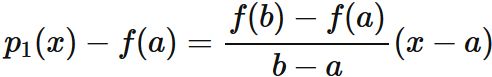 が成り立つ。
台形公式はこの直線を区間 $[a, b]$ に渡って積分すると得られる。
すなわち、
が成り立つ。
台形公式はこの直線を区間 $[a, b]$ に渡って積分すると得られる。
すなわち、
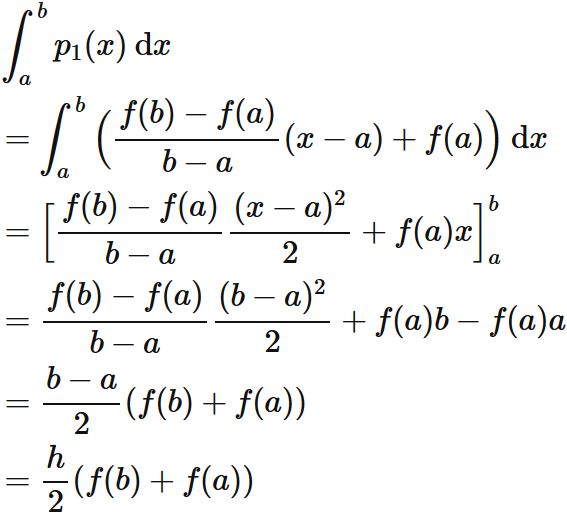 である。
である。
積分
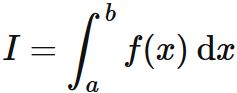


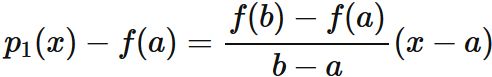
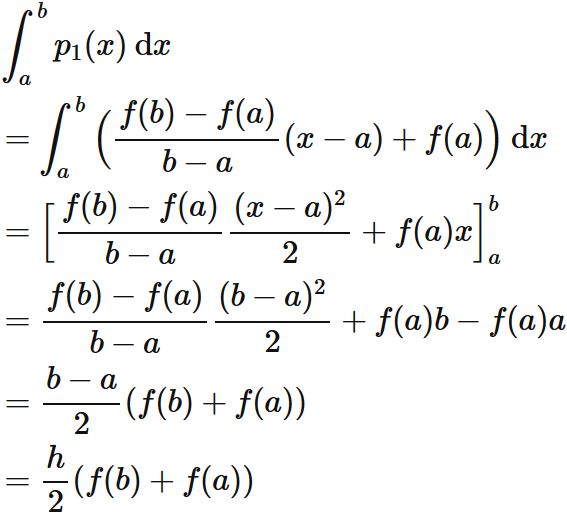
具体例: (台形公式)
積分
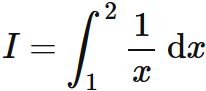
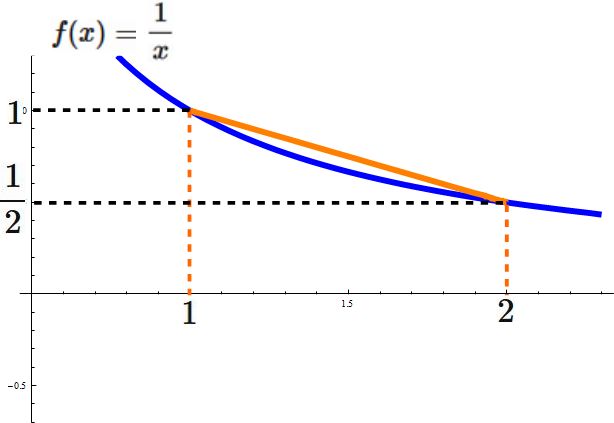
解答例
$f(x) = \frac{1}{x}$ とすると、
 であり、積分区間の幅 $h$ は、
であり、積分区間の幅 $h$ は、
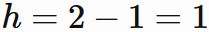 であるので、
台形公式を用いると、
であるので、
台形公式を用いると、
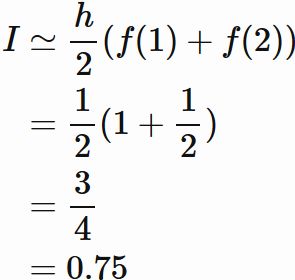 である。真の値は
である。真の値は
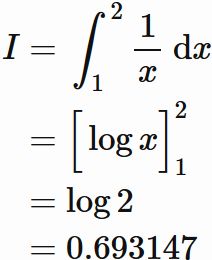 であるので、両者違いの割合は、
であるので、両者違いの割合は、
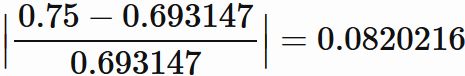 である。
である。
なお、実際には本題のように値の求まる積分ではなく、 値の求まらない積分に対して公式が使われる。
$f(x) = \frac{1}{x}$ とすると、

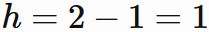
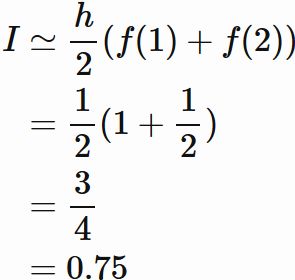
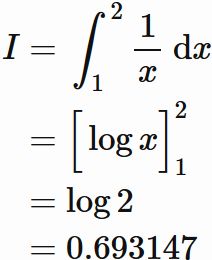
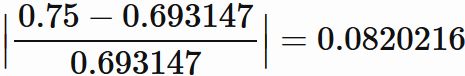
なお、実際には本題のように値の求まる積分ではなく、 値の求まらない積分に対して公式が使われる。
シンプソン公式
積分
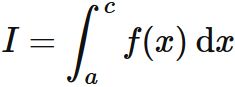

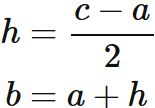
解説
積分
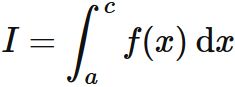 の被積分関数 $f(x)$ を $3$ 点
の被積分関数 $f(x)$ を $3$ 点
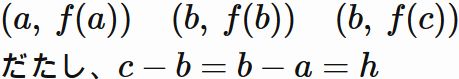 $$
\tag{1}
$$
を通る二次関数で近似し、
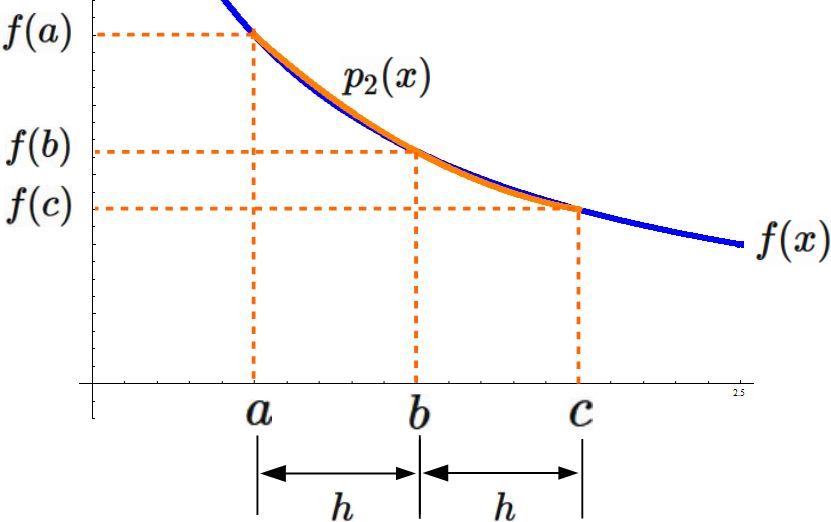
その積分によって $I$ の近似値を与える公式をシンプソン公式という(下図)。
$$
\tag{1}
$$
を通る二次関数で近似し、
その積分によって $I$ の近似値を与える公式をシンプソン公式という(下図)。
 シンプソン公式を求める。
$3$ 点 $(1)$ を通る 二次関数を $p_{2}(x)$ とすると、
ラグランジュの補間公式によって、
シンプソン公式を求める。
$3$ 点 $(1)$ を通る 二次関数を $p_{2}(x)$ とすると、
ラグランジュの補間公式によって、
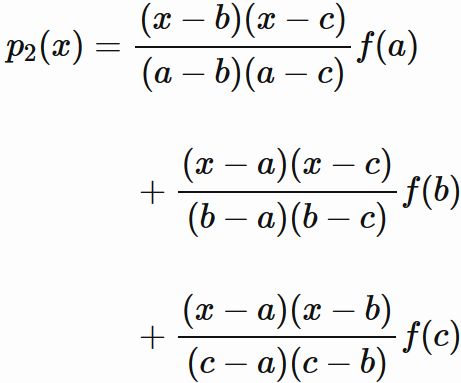 である。
シンプソン公式はこの二次関数を区間 $[a, c]$ に渡って積分すると得られる。
すなわち、
である。
シンプソン公式はこの二次関数を区間 $[a, c]$ に渡って積分すると得られる。
すなわち、
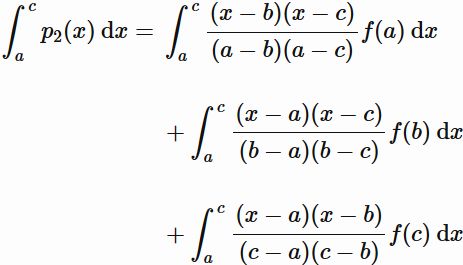 $$
\tag{2}
$$
を計算すれば得られる。
$$
\tag{2}
$$
を計算すれば得られる。
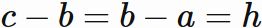 であるので、$c = a + 2h$ である。
これを用いて上記の積分を計算すると、
であるので、$c = a + 2h$ である。
これを用いて上記の積分を計算すると、
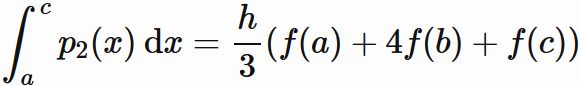 $$
\tag{3}
$$
が得られる
(計算の詳細は以下のボタンから閲覧可能)。
$$
\tag{3}
$$
が得られる
(計算の詳細は以下のボタンから閲覧可能)。
積分
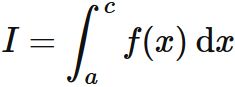
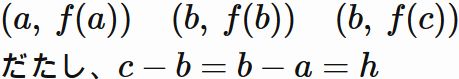

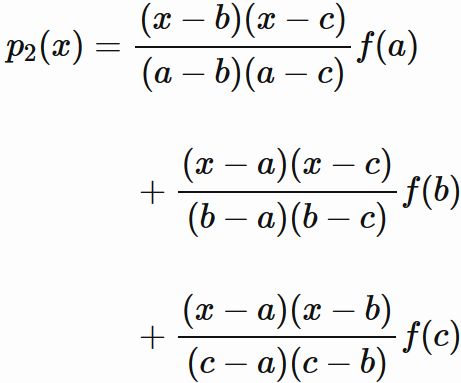
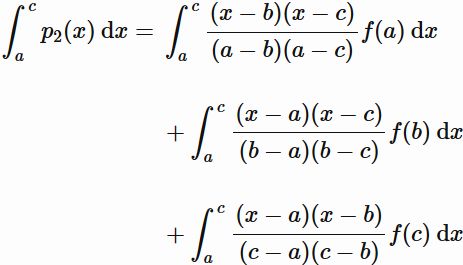
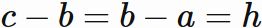
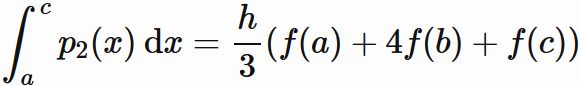
証明
$(2)$ の各積分を計算すると、
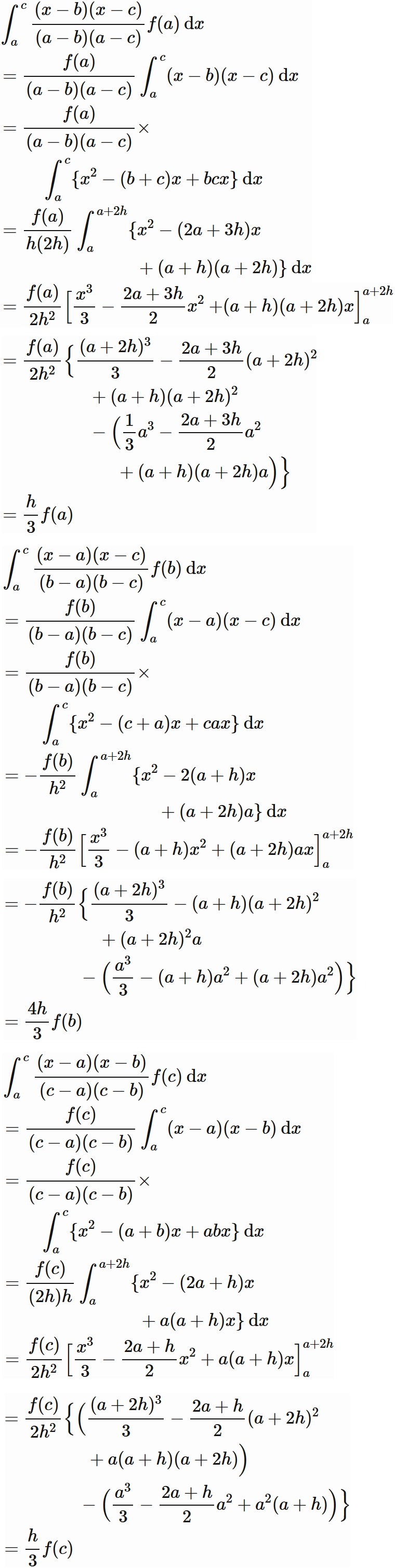 であるので、
であるので、
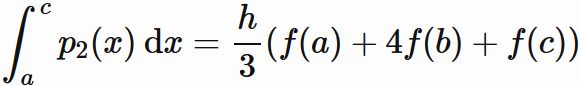 が成り立つ。
が成り立つ。
$(2)$ の各積分を計算すると、
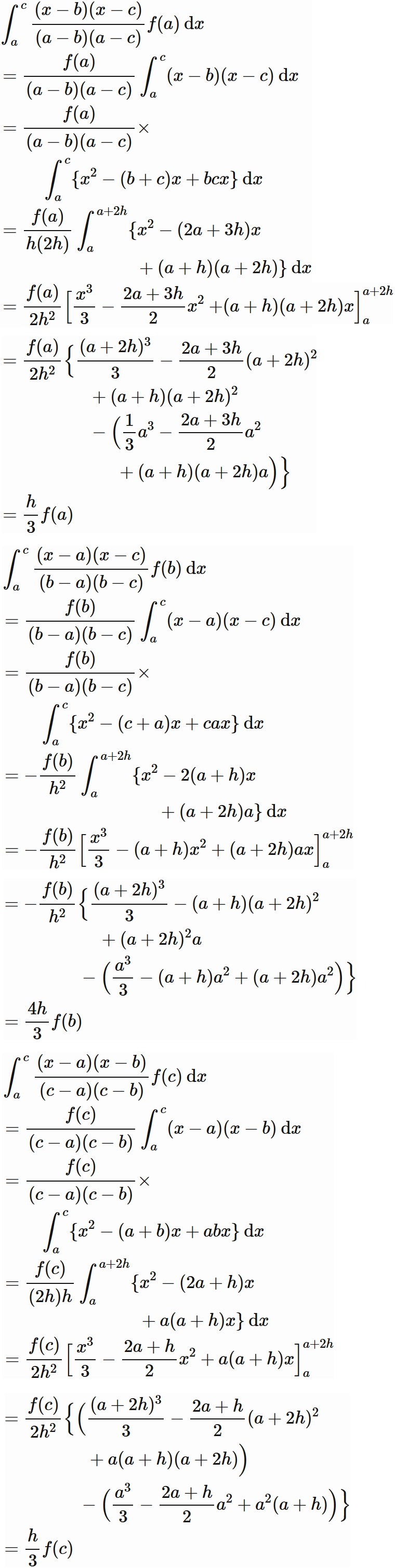
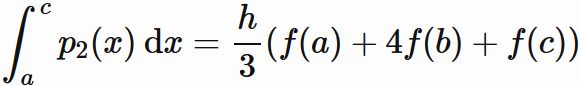
具体例: (シンプソン公式)
積分
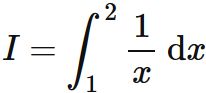
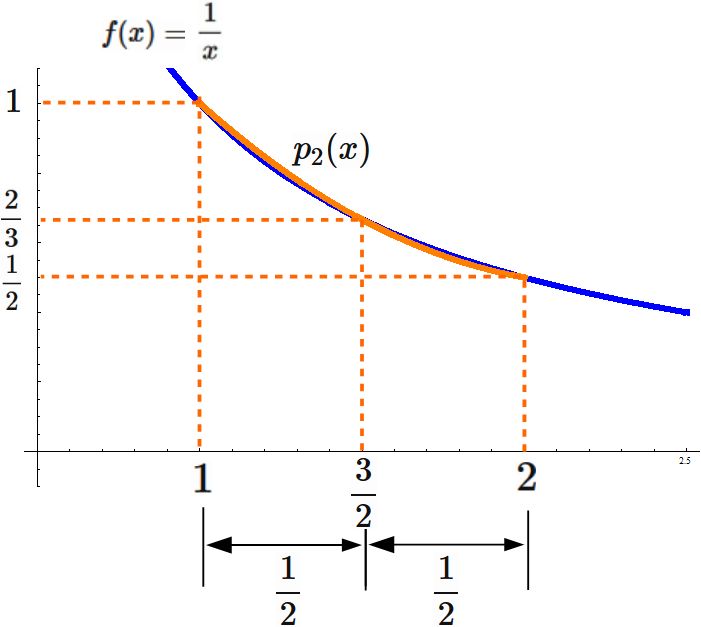
解答例
$f(x) = \frac{1}{x}$ とすると、
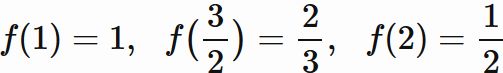 であり、積分区間の幅 $h$ は、
であり、積分区間の幅 $h$ は、
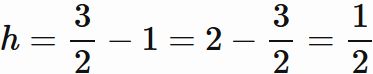 であるので、
シンプソン公式を用いると、
であるので、
シンプソン公式を用いると、
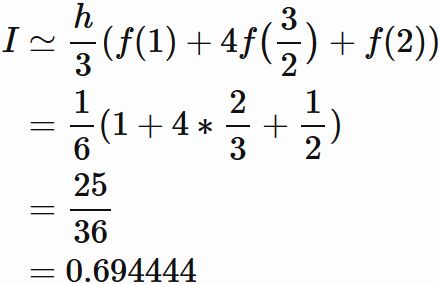 である。真の値は
である。真の値は
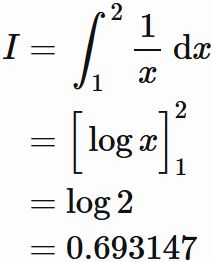 であるので、違いの割合は、
であるので、違いの割合は、
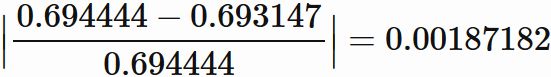 である。
なお、実際には本題のように値の求まる積分ではなく、
値の求まらない積分に対して公式が使われる。
である。
なお、実際には本題のように値の求まる積分ではなく、
値の求まらない積分に対して公式が使われる。
$f(x) = \frac{1}{x}$ とすると、
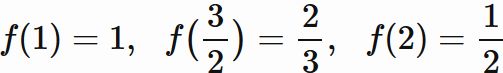
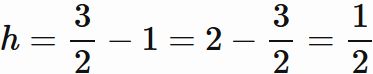
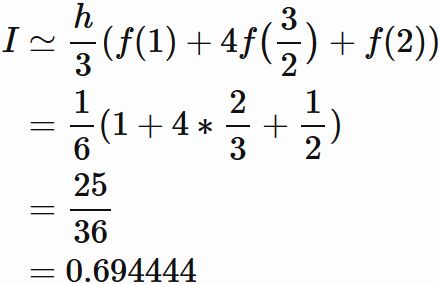
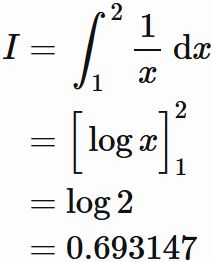
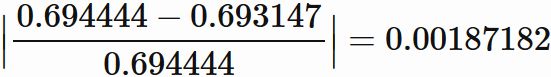
合成台形公式
積分
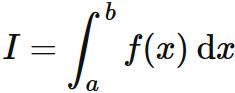
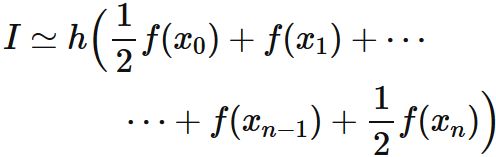
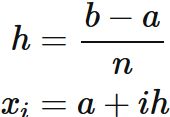
解説
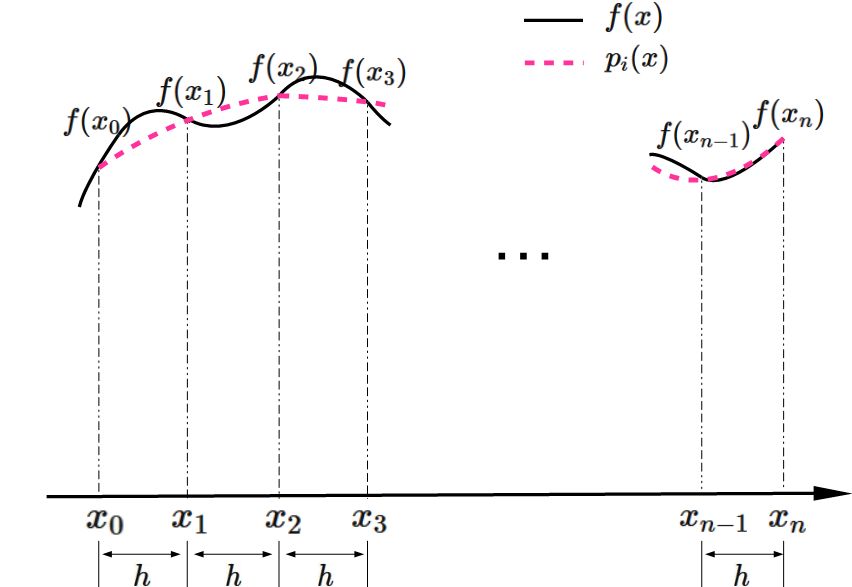
積分区間 $[ a,\hspace{1mm} b]$ を $n$ 個の小区間に等分割し、 各小区間に対して、台形公式を適用し、 積分 $I$ の近似値を求める。
各区間の幅 $h$ は
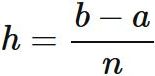 である。ここで
である。ここで
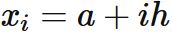 とすると、
各 $x_{i}$ は小区間の境界である。
とすると、
各 $x_{i}$ は小区間の境界である。
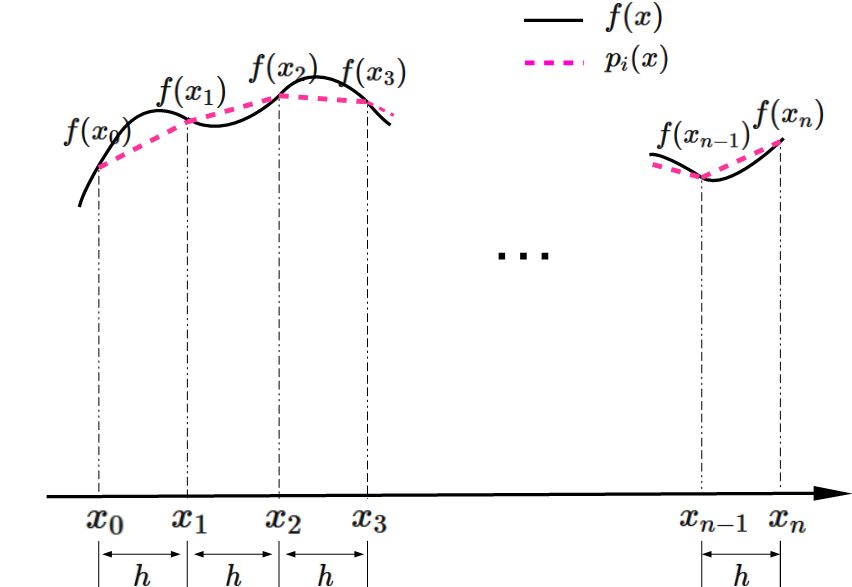 積分 $I$ を
小区間 $[ x_{i}, \hspace{1mm} x_{i+1}]$ に分割し、
それぞれの小区間の積分を近似する台形公式を $I_{i}$ とすると、
積分 $I$ を
小区間 $[ x_{i}, \hspace{1mm} x_{i+1}]$ に分割し、
それぞれの小区間の積分を近似する台形公式を $I_{i}$ とすると、
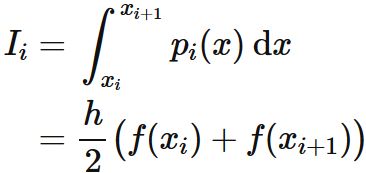 である。ここで $p_{i}(x)$ は二点
である。ここで $p_{i}(x)$ は二点
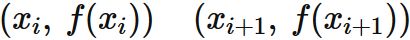 を通る直線である。
を通る直線である。
これより、 積分 $I$ を各区間に分割し、 それぞれ対して台形公式による近似を行うと、
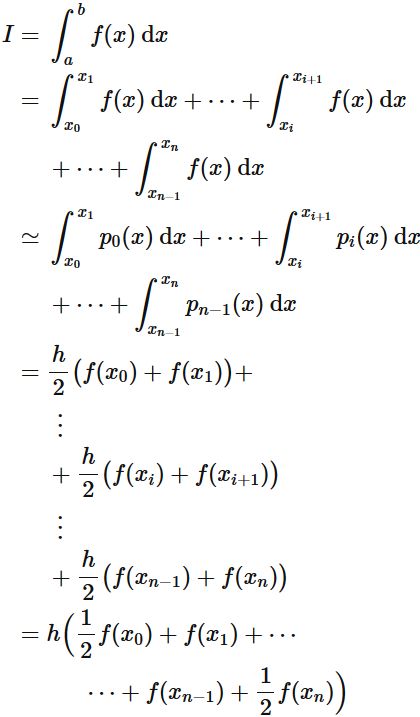 である。
最後の式は、
被積分関数 $f(x)$ の各 $x_{i}$ における値 (すなわち $f(x_{i})$)
さえ分かれば、
積分 $I$ の近似値求められることを表している。
である。
最後の式は、
被積分関数 $f(x)$ の各 $x_{i}$ における値 (すなわち $f(x_{i})$)
さえ分かれば、
積分 $I$ の近似値求められることを表している。
積分区間 $[ a,\hspace{1mm} b]$ を $n$ 個の小区間に等分割し、 各小区間に対して、台形公式を適用し、 積分 $I$ の近似値を求める。
各区間の幅 $h$ は
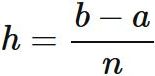
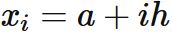

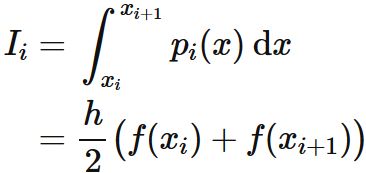
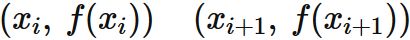
これより、 積分 $I$ を各区間に分割し、 それぞれ対して台形公式による近似を行うと、
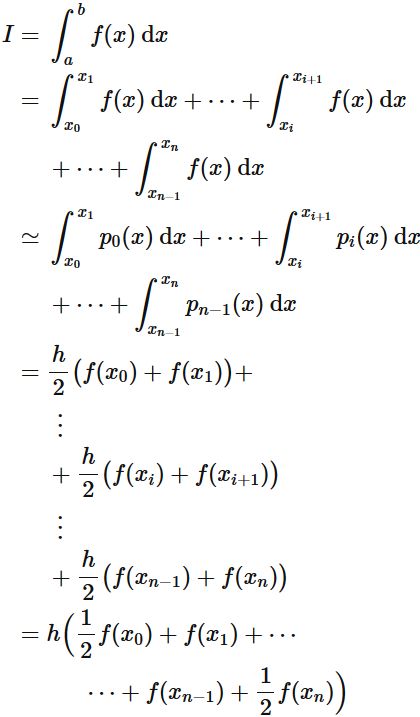
合成シンプソン公式
積分
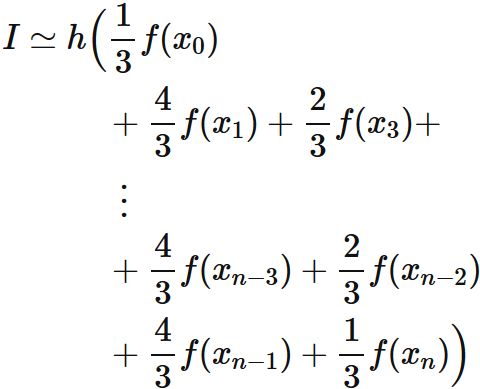
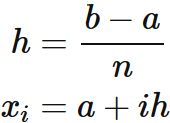
解説
積分区間 $[ a,\hspace{1mm} b]$ を偶数 $n$ 個の小区間に等分割し、 連なる $2$ 個ずつの小区間に対して、 シンプソン公式を適用し、 積分 $I$ の近似値を求める。
各区間の幅 $h$ は
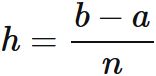 である。ここで
である。ここで
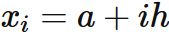 とすると、
各 $x_{i}$ は小区間の境界である。
とすると、
各 $x_{i}$ は小区間の境界である。
 積分 $I$ を
小区間 $[ x_{i}, \hspace{1mm} x_{i+1}]$ と $[ x_{i+1}, \hspace{1mm} x_{i+2}]$ を合わせた区間 $[ x_{i}, \hspace{1mm} x_{i+2}]$ に分割し、
この区間の積分を近似する台形公式を $I_{i}$ とすると、
積分 $I$ を
小区間 $[ x_{i}, \hspace{1mm} x_{i+1}]$ と $[ x_{i+1}, \hspace{1mm} x_{i+2}]$ を合わせた区間 $[ x_{i}, \hspace{1mm} x_{i+2}]$ に分割し、
この区間の積分を近似する台形公式を $I_{i}$ とすると、
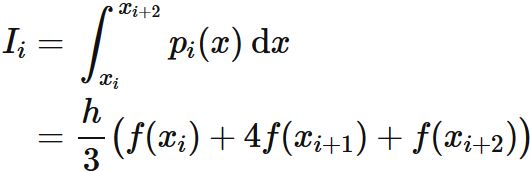 である。ここで $p_{i}(x)$ は $3$ 点
である。ここで $p_{i}(x)$ は $3$ 点
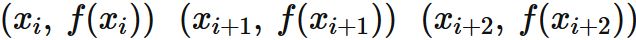 を通る二次関数である。
を通る二次関数である。
これより、 積分 $I$ を分割し、 それぞれ対してシンプソン公式による近似を行うと、
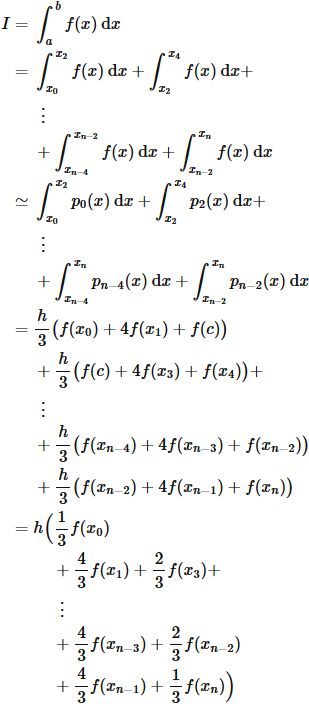 である。
最後の式は被積分関数 $f(x)$ の各 $x_{i}$ における値 (すなわち $f(x_{i})$)
さえ分かれば、
積分 $I$ の近似値求められることを表している。
である。
最後の式は被積分関数 $f(x)$ の各 $x_{i}$ における値 (すなわち $f(x_{i})$)
さえ分かれば、
積分 $I$ の近似値求められることを表している。
積分区間 $[ a,\hspace{1mm} b]$ を偶数 $n$ 個の小区間に等分割し、 連なる $2$ 個ずつの小区間に対して、 シンプソン公式を適用し、 積分 $I$ の近似値を求める。
各区間の幅 $h$ は
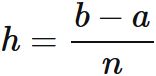
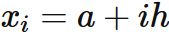

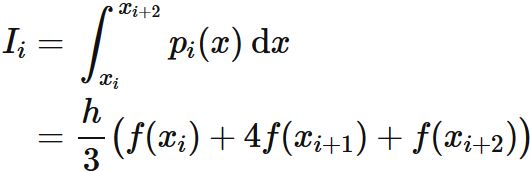
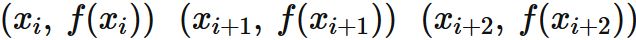
これより、 積分 $I$ を分割し、 それぞれ対してシンプソン公式による近似を行うと、
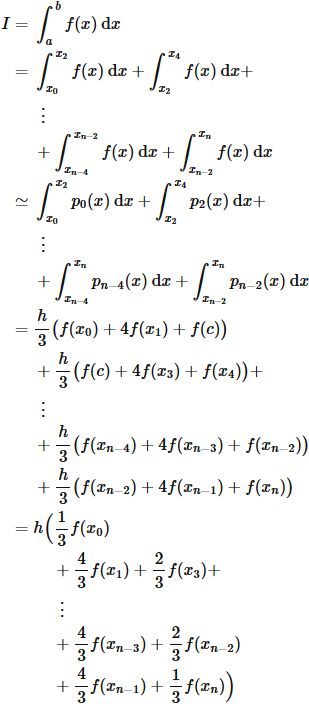
ニュートン・コーツの公式
積分

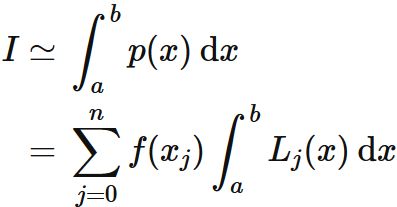
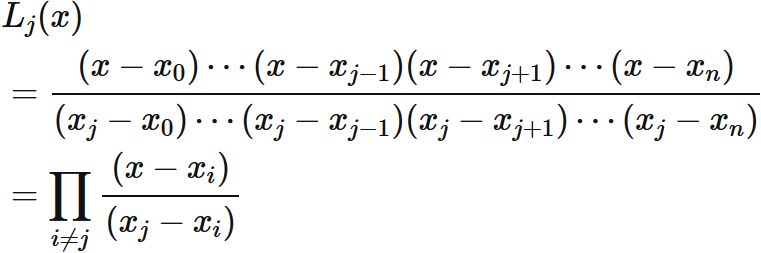

ニュートン・コーツの公式の公式の $n=1$ の場合が台形公式であり、 $n=2$ の場合がシンプソンの公式である。
解説
積分
 の被積分関数 $f(x)$ を $n+1$ 点
の被積分関数 $f(x)$ を $n+1$ 点
 $$
\tag{1}
$$
を通る $n$ 次関数で近似し、
その積分によって $I$ の近似値を与える公式をニュートン・コーツ公式という(下図)。
ニュートン・コーツ公式を求める。
$$
\tag{1}
$$
を通る $n$ 次関数で近似し、
その積分によって $I$ の近似値を与える公式をニュートン・コーツ公式という(下図)。
ニュートン・コーツ公式を求める。
$n+1$ 点を通る $n$ 次関数 $p_{x}$ はラグランジュの補間によって、
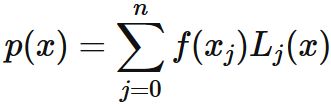 である。
ここで $L_{j}(x)$ は $n$ 次関数
である。
ここで $L_{j}(x)$ は $n$ 次関数
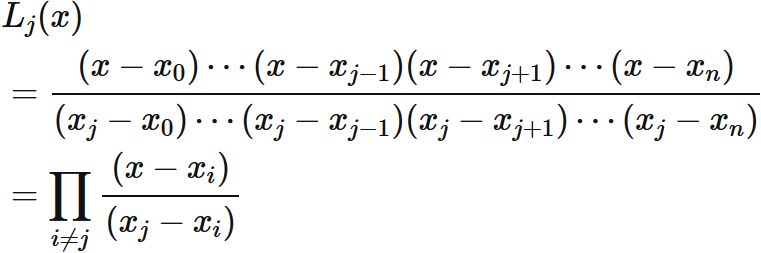 である。
これより、
である。
これより、
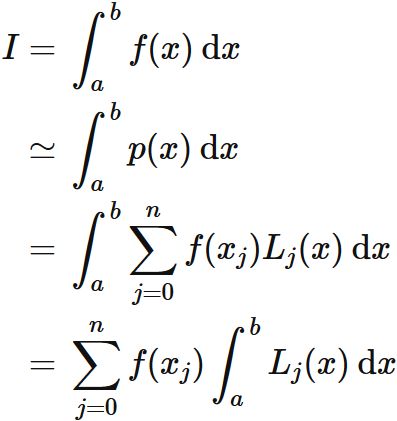 とニュートン・コーツの公式が求まる。
とニュートン・コーツの公式が求まる。
$n=1$ の場合、
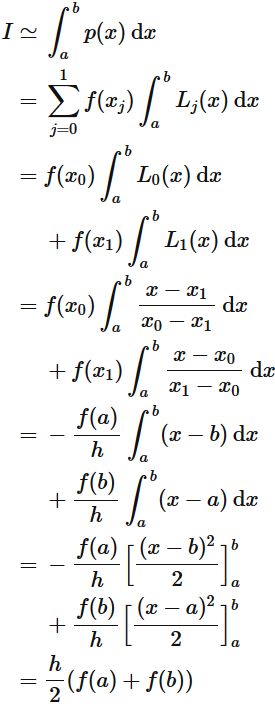 と台形公式が求まる。
同じように $n=2$ の場合にはシンプソンの公式が求まる。
と台形公式が求まる。
同じように $n=2$ の場合にはシンプソンの公式が求まる。
積分

$n+1$ 点を通る $n$ 次関数 $p_{x}$ はラグランジュの補間によって、
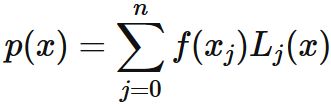
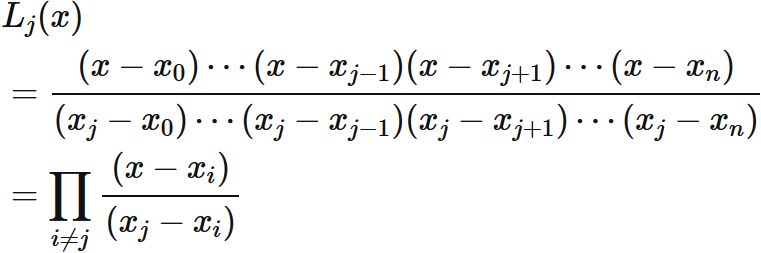
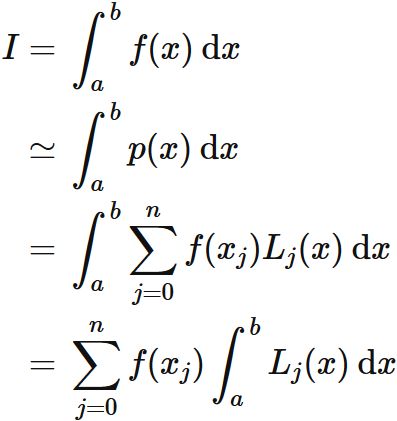
$n=1$ の場合、