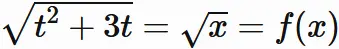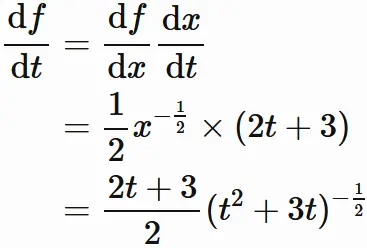合成関数の微分とは?
本ページでは、合成関数の微分の公式の丁寧な証明と、簡単な具体例が記されています。
合成関数の微分
関数 $x(t)$ が $t$ の区間 $I$ で微分可能であるとする。
また、関数
$f(x)$ が $x$ の区間 $J$ で微分可能であるとする。
このとき、
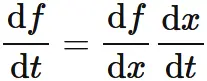
証明
はじめに、
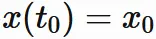 とする。また
とする。また
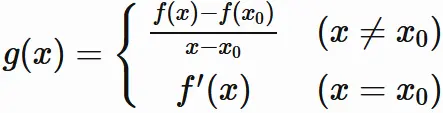 $$
\tag{1}
$$
とする。このとき、
$$
\tag{1}
$$
とする。このとき、
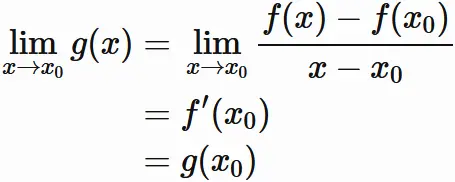 $$
\tag{2}
$$
が成り立つので、
$g(x)$ は連続である。
また、
$(1)$ より
$$
\tag{2}
$$
が成り立つので、
$g(x)$ は連続である。
また、
$(1)$ より
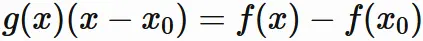 であるので、
$t \neq t_{0}$ の場合
であるので、
$t \neq t_{0}$ の場合
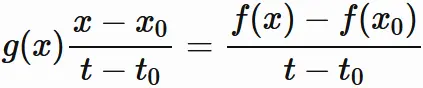 が成り立つが、
これと積の極限の性質から
が成り立つが、
これと積の極限の性質から
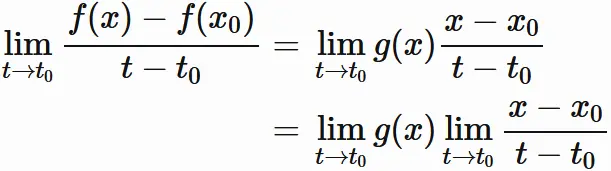 $$
\tag{3}
$$
が成り立つ。
$$
\tag{3}
$$
が成り立つ。
ここで、 $x(t)$ が微分可能であることから、 $x(t)$ は連続関数であるため (「微分可能⇒連続」を参考)、
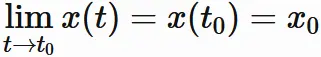 であることと $(2)$ から、合成関数の極限の性質により、
であることと $(2)$ から、合成関数の極限の性質により、
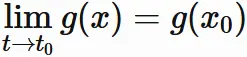 が成り立つ。
これと $(1)$ より、
が成り立つ。
これと $(1)$ より、
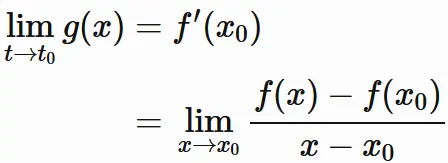 である。これを $(3)$ に代入すると、
である。これを $(3)$ に代入すると、
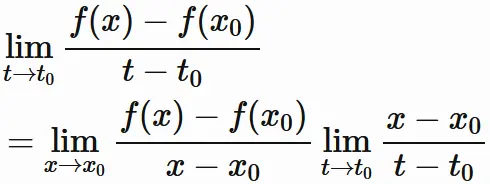 を得る。
導関数の定義から
を得る。
導関数の定義から
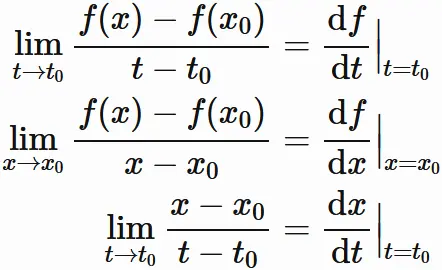 であるので、
であるので、
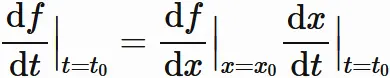 を得る。ここで $x(t_{0})=x_{0}$ であるが、
この部分を明示的に記述しないように表すと、
を得る。ここで $x(t_{0})=x_{0}$ であるが、
この部分を明示的に記述しないように表すと、
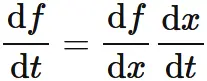 である。
である。
補足
素直に考えると、
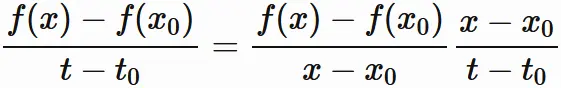 と表して、両辺の極限をとれば、合成関数の微分の公式を得られるが、
上式は $x=x_{0}$ の場合に表せないので、上のような手のかかる証明を展開している。
と表して、両辺の極限をとれば、合成関数の微分の公式を得られるが、
上式は $x=x_{0}$ の場合に表せないので、上のような手のかかる証明を展開している。
はじめに、
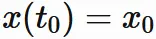
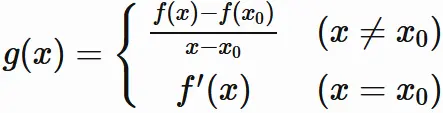
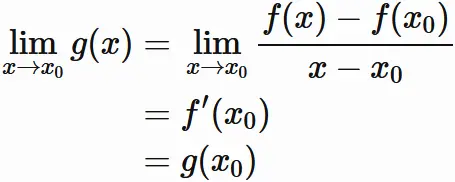
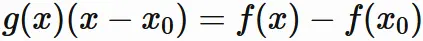
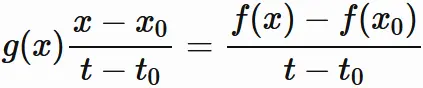
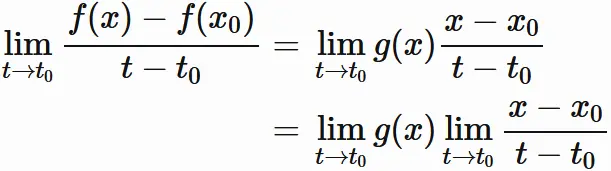
ここで、 $x(t)$ が微分可能であることから、 $x(t)$ は連続関数であるため (「微分可能⇒連続」を参考)、
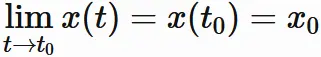
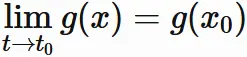
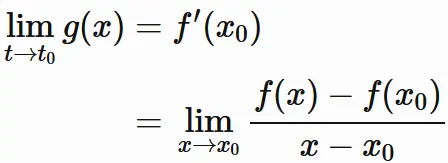
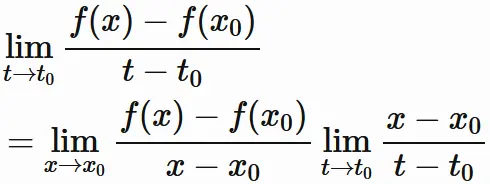
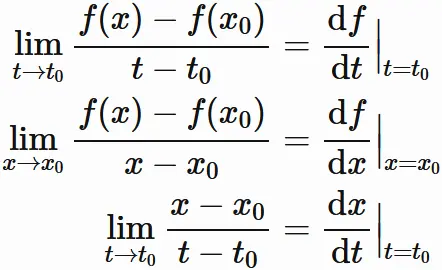
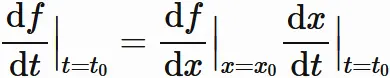
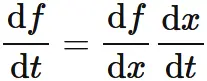
補足
素直に考えると、
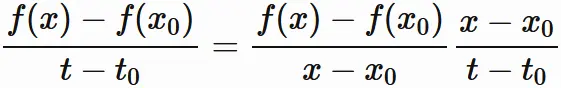
具体例
(1)
$ e^{t^{2}}$ を $t$ で微分せよ。
(2) $ \cos (\sin t)$ を $t$ で微分せよ。
(3) $ \sqrt{t^{2}+3t }$ を $t$ で微分せよ。
証明
(1) $t^{2} = x$ とし、$f(x) = e^x$ とすると、
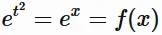 である。
そこで合成関数の微分の公式を用いると、
である。
そこで合成関数の微分の公式を用いると、
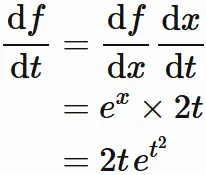 を得る。
を得る。
(2) $ \sin t = x$ とし、$f(x) = \cos x$ とすると、
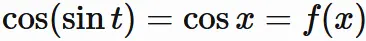 である。
そこで合成関数の微分の公式を用いると、
である。
そこで合成関数の微分の公式を用いると、
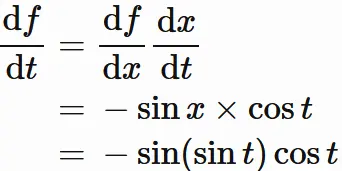 を得る。
を得る。
(3) $ t^{2}+3t = x$ とし、$f(x) = \sqrt{x}$ とすると、
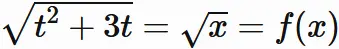 である。
そこで合成関数の微分の公式を用いると、
である。
そこで合成関数の微分の公式を用いると、
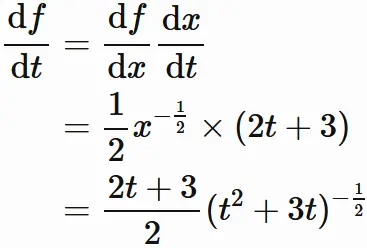 を得る。
を得る。
(1) $t^{2} = x$ とし、$f(x) = e^x$ とすると、
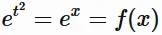
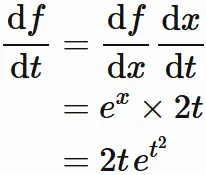
(2) $ \sin t = x$ とし、$f(x) = \cos x$ とすると、
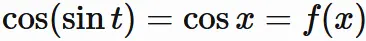
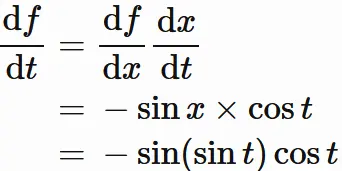
(3) $ t^{2}+3t = x$ とし、$f(x) = \sqrt{x}$ とすると、