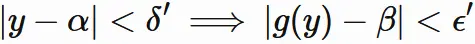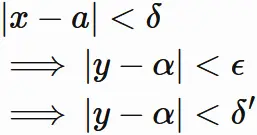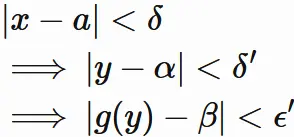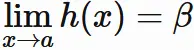関数の極限とは?
本ページでは、関数の極限の定義と基本的な性質(和の極限、積の極限、商の極限、定数倍の極限、合成関数の極限)の丁寧な証明が記されています。
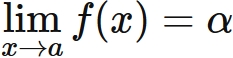
関数の極限と極限値とは?
関数の極限を表す記号
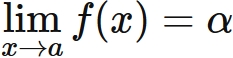
すなわち、 任意の正の数 $\epsilon$ に対して、 ある正の数 $\delta$ が存在し、
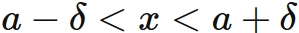
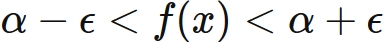
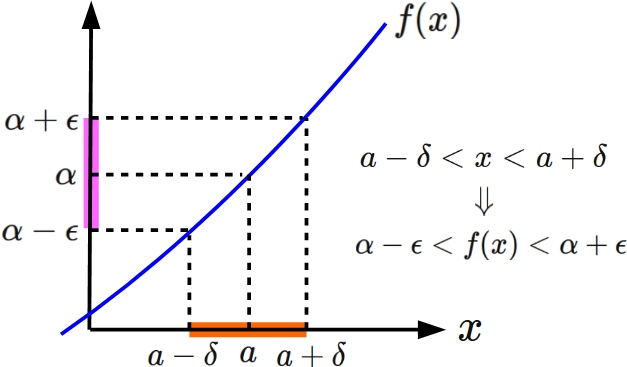
$(1)$ と $(2)$を書き直すと、それぞれ
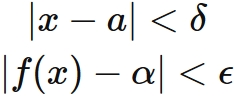
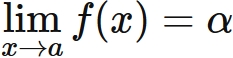
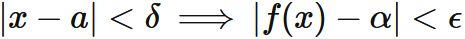
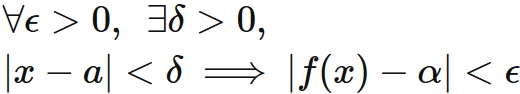
この性質を満たす $\alpha$ を関数 $f(x)$ の $x \rightarrow a$ における 極限(値)という。
和の極限
関数の和の極限は、それぞれの極限値の和に等しい。
すなわち、
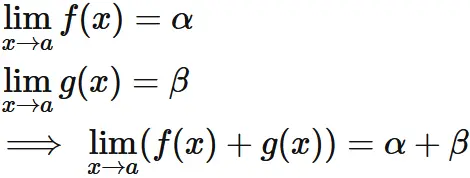
証明
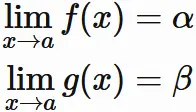 であるとする。
極限の定義より、
これは任意の正の数
$\epsilon_{f}$
に対して
であるとする。
極限の定義より、
これは任意の正の数
$\epsilon_{f}$
に対して
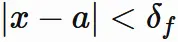 $$
\tag{2.1}
$$
であるならば、
$$
\tag{2.1}
$$
であるならば、
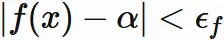 $$
\tag{2.2}
$$
が成り立つ正の数
$\delta_{f}$
が存在する。
また、
任意の正の数
$\epsilon_{g}$
に対して、
$$
\tag{2.2}
$$
が成り立つ正の数
$\delta_{f}$
が存在する。
また、
任意の正の数
$\epsilon_{g}$
に対して、
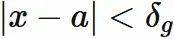 $$
\tag{2.3}
$$
であるならば、
$$
\tag{2.3}
$$
であるならば、
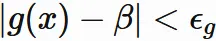 $$
\tag{2.4}
$$
が成り立つある正の数
$\delta_{g}$ が存在する。
$$
\tag{2.4}
$$
が成り立つある正の数
$\delta_{g}$ が存在する。
ここで
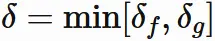 と $\delta$
を定義すると、
と $\delta$
を定義すると、
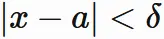 $$
\tag{2.5}
$$
であるならば、
$(2.1)$
と
$(2.3)$
が成り立つので、
$(2.2)$ と $(2.4)$ と
三角不等式により、
$$
\tag{2.5}
$$
であるならば、
$(2.1)$
と
$(2.3)$
が成り立つので、
$(2.2)$ と $(2.4)$ と
三角不等式により、
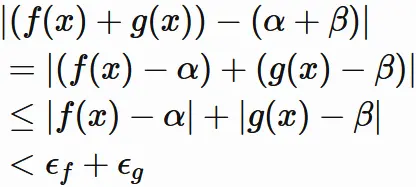 が成り立つ。ここで、
が成り立つ。ここで、
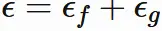 と
$\epsilon$
を定義すると、
$\epsilon_{f}$ と $\epsilon_{g}$ は任意の正の数であるので、
$\epsilon$
もまた任意の正の数である。
ゆえに、
任意の正の数
$\epsilon$
に対して、
$(2.5)$
であるならば、
と
$\epsilon$
を定義すると、
$\epsilon_{f}$ と $\epsilon_{g}$ は任意の正の数であるので、
$\epsilon$
もまた任意の正の数である。
ゆえに、
任意の正の数
$\epsilon$
に対して、
$(2.5)$
であるならば、
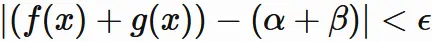 が成り立つ正の数 $\delta$ が存在する。
したがって
が成り立つ正の数 $\delta$ が存在する。
したがって
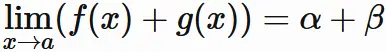 である。
である。
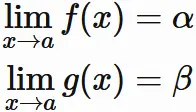
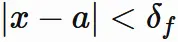
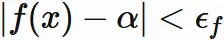
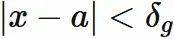
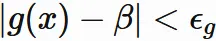
ここで
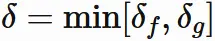
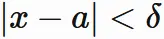
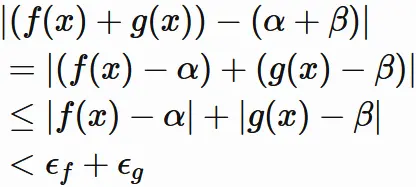
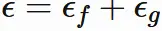
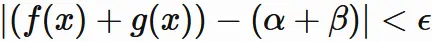
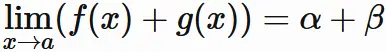
積の極限
関数の積の極限は、それぞれの極限値の積に等しい。
すなわち、
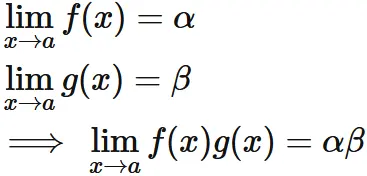
証明
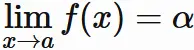 であるとする。
極限の定義より
任意の正の $\epsilon_{f}$ に対して、
であるとする。
極限の定義より
任意の正の $\epsilon_{f}$ に対して、
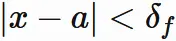 $$
\tag{3.1}
$$
であるならば、
$$
\tag{3.1}
$$
であるならば、
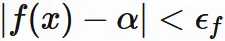 $$
\tag{3.2}
$$
が成り立つ
正の数 $\delta_{f}$ が存在する。
$(3.2)$ は
$$
\tag{3.2}
$$
が成り立つ
正の数 $\delta_{f}$ が存在する。
$(3.2)$ は
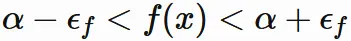 と表されるので、
$|f(x)|$ は $|\alpha + \epsilon_{f}|$ よりも小さいか、
$|\alpha - \epsilon_{f}|$ よりも小さいかのどちらかである。
したがって、これらのうちの大きい方を $M$ と定義すると、
すなわち、
と表されるので、
$|f(x)|$ は $|\alpha + \epsilon_{f}|$ よりも小さいか、
$|\alpha - \epsilon_{f}|$ よりも小さいかのどちらかである。
したがって、これらのうちの大きい方を $M$ と定義すると、
すなわち、
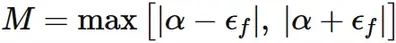 とすると、
とすると、
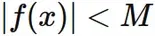 $$
\tag{3.3}
$$
が成り立つ。
$$
\tag{3.3}
$$
が成り立つ。
一方、
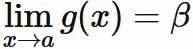 であるとすると、
極限の定義より
任意の正の $\epsilon_{g}$ に対して、
であるとすると、
極限の定義より
任意の正の $\epsilon_{g}$ に対して、
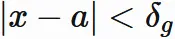 $$
\tag{3.4}
$$
であるならば、
$$
\tag{3.4}
$$
であるならば、
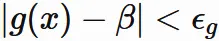 $$
\tag{3.5}
$$
が成り立つ正の数 $\delta_{g}$ が存在する。
$$
\tag{3.5}
$$
が成り立つ正の数 $\delta_{g}$ が存在する。
ここで、 $\delta_{f}$ と $\delta_{g}$ の小さいほうを $\delta$ とすると、
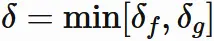 と $\delta$ を定義すると、
と $\delta$ を定義すると、
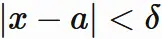 $$
\tag{3.6}
$$
であるならば、
$(3.1)$ と $(3.4)$
が成り立つので、
$(3.2)$
$(3.3)$
$(3.5)$ と三角不等式により、
$$
\tag{3.6}
$$
であるならば、
$(3.1)$ と $(3.4)$
が成り立つので、
$(3.2)$
$(3.3)$
$(3.5)$ と三角不等式により、
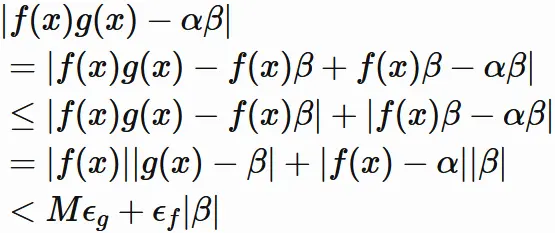 $$
\tag{3.7}
$$
が成り立つ。
ここで、
$$
\tag{3.7}
$$
が成り立つ。
ここで、
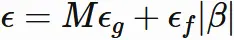 と置くと、
$\epsilon_{f}$ と $\epsilon_{g}$ は任意の正の数であるので、
$\epsilon$ もまた任意の正の数である。
と置くと、
$\epsilon_{f}$ と $\epsilon_{g}$ は任意の正の数であるので、
$\epsilon$ もまた任意の正の数である。
以上から、 任意の正の数 $\epsilon$ に対して、 $(3.6)$ であるならば、
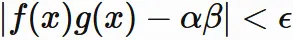 が成り立つ正の数 $\delta$ が存在する。
よって、
が成り立つ正の数 $\delta$ が存在する。
よって、
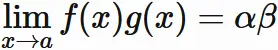 である。
である。
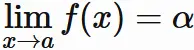
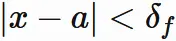
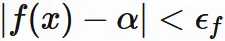
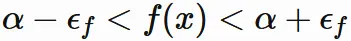
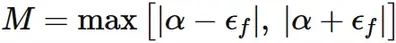
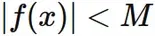
一方、
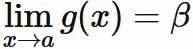
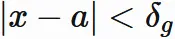
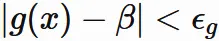
ここで、 $\delta_{f}$ と $\delta_{g}$ の小さいほうを $\delta$ とすると、
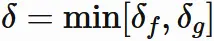
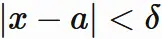
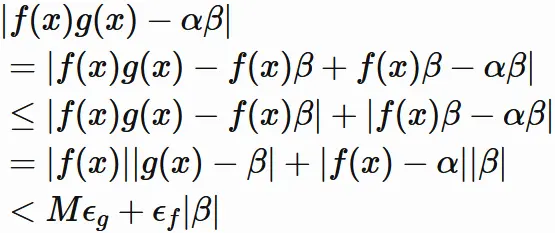
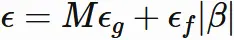
以上から、 任意の正の数 $\epsilon$ に対して、 $(3.6)$ であるならば、
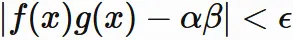
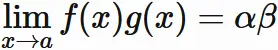
商の極限
関数の商の極限は、それぞれの極限値の商に等しい。
すなわち、
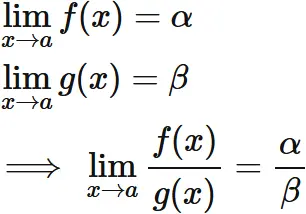
証明
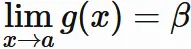 であるとする。
極限の定義より、
任意の正の $\epsilon_{g}$ に対して、
であるとする。
極限の定義より、
任意の正の $\epsilon_{g}$ に対して、
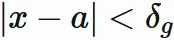 $$
\tag{4.1}
$$
であるならば、
$$
\tag{4.1}
$$
であるならば、
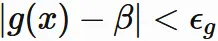 $$
\tag{4.2}
$$
が成り立つ正の数 $\delta_{g}$ が存在する。
$(4.2)$ は
$$
\tag{4.2}
$$
が成り立つ正の数 $\delta_{g}$ が存在する。
$(4.2)$ は
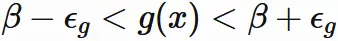 と表されるので、
$|g(x)|$ は $|\beta - \epsilon_{g}|$ よりも大きいか、
$|\beta + \epsilon_{g}|$ よりも大きいかのどちらかである。
したがって、
これらのうちの小さい方を $L$ と定義すると、
すなわち、
と表されるので、
$|g(x)|$ は $|\beta - \epsilon_{g}|$ よりも大きいか、
$|\beta + \epsilon_{g}|$ よりも大きいかのどちらかである。
したがって、
これらのうちの小さい方を $L$ と定義すると、
すなわち、
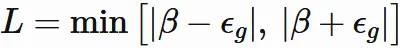 とすると、
とすると、
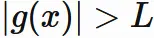 $$
\tag{4.3}
$$
が成り立つ。
$$
\tag{4.3}
$$
が成り立つ。
これらを踏まえて初めに
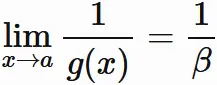 を証明する。
$(4.1)$
であるならば、
$(4.3)$ と $(4.2)$ を満たす $\delta_{g}$ が存在する。
これより、
$(4.1)$
であるならば、
を証明する。
$(4.1)$
であるならば、
$(4.3)$ と $(4.2)$ を満たす $\delta_{g}$ が存在する。
これより、
$(4.1)$
であるならば、
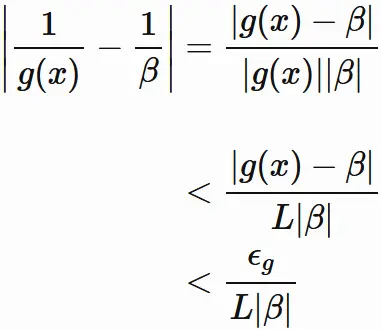 $$
\tag{4.4}
$$
が成り立つ
$\delta_{g}$ が存在することになる。
ここで、
$$
\tag{4.4}
$$
が成り立つ
$\delta_{g}$ が存在することになる。
ここで、
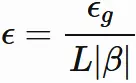 と定義すると、
$\epsilon_{g}$ が任意の正の数であるので、
$\epsilon$ もまた任意の正の数である。
したがって、
任意の正の数 $\epsilon$ に対して、
$(4.1)$
であるならば、
と定義すると、
$\epsilon_{g}$ が任意の正の数であるので、
$\epsilon$ もまた任意の正の数である。
したがって、
任意の正の数 $\epsilon$ に対して、
$(4.1)$
であるならば、
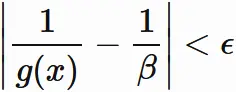 が成り立つ正の数 $\delta_{g}$ が存在することになる。
よって、
が成り立つ正の数 $\delta_{g}$ が存在することになる。
よって、
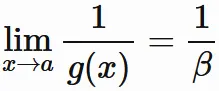 $$
\tag{4.5}
$$
である。
$$
\tag{4.5}
$$
である。
続いて
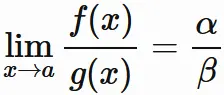 を証明する。
$(4.5)$ において
を証明する。
$(4.5)$ において
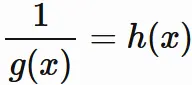 $$
\tag{4.6}
$$
と表すと、
$$
\tag{4.6}
$$
と表すと、
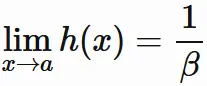 である。
ここで
である。
ここで
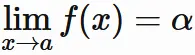 が成り立つとすると、
関数の積の極限の性質より、
が成り立つとすると、
関数の積の極限の性質より、
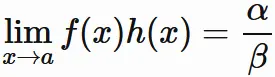 である。したがって、
である。したがって、
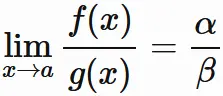 である。
である。
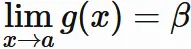
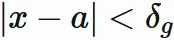
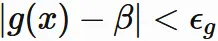
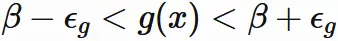
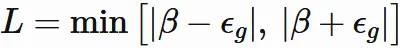
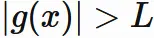
これらを踏まえて初めに
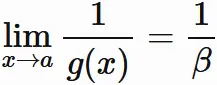
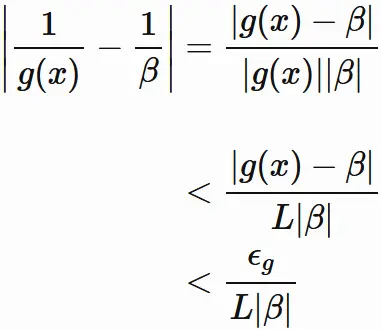
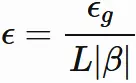
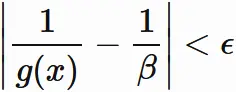
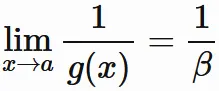
続いて
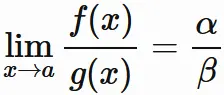
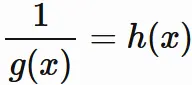
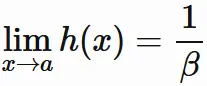
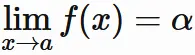
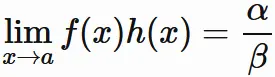
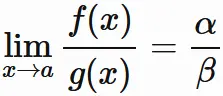
定数倍の極限
関数の定数倍の極限は、極限値の定数倍に等しい。
すなわち、
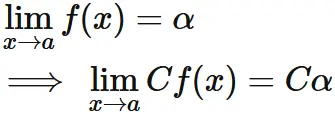
証明
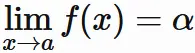 であるとする。
極限の定義より、
これは
任意の正の数
$\epsilon$
に対して、
であるとする。
極限の定義より、
これは
任意の正の数
$\epsilon$
に対して、
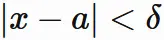 $$
\tag{5.1}
$$
であるならば
$$
\tag{5.1}
$$
であるならば
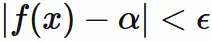 が成り立つ正の数
$\delta$
が存在することを表している。
これより、
$(5.1)$
ならば
が成り立つ正の数
$\delta$
が存在することを表している。
これより、
$(5.1)$
ならば
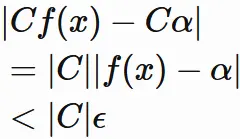 が成り立つ。
が成り立つ。
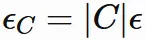 と置くと、
$\epsilon$
が任意の正の数であるので、
$\epsilon_{C}$
もまた任意の正の数である。
と置くと、
$\epsilon$
が任意の正の数であるので、
$\epsilon_{C}$
もまた任意の正の数である。
ゆえに、 任意の正の数 $\epsilon_{C} $ に対して、 $(5.1)$ であるならば、
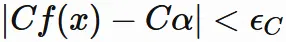 が成り立つ正の数 $\delta$ が存在することになる。
したがって、
が成り立つ正の数 $\delta$ が存在することになる。
したがって、
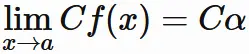 である。
である。
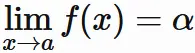
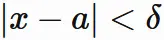
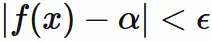
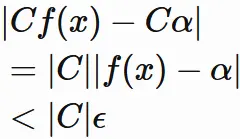
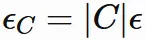
ゆえに、 任意の正の数 $\epsilon_{C} $ に対して、 $(5.1)$ であるならば、
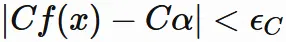
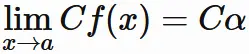
合成関数の極限
関数 $f$ と関数 $g$ の合成関数を $h$ とする。
すなわち、
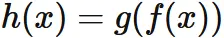
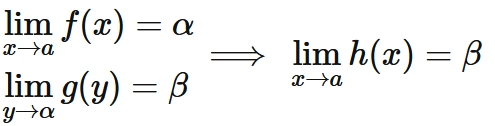
証明
関数の極限の定義より
 であるとは、次の命題が成り立つことである。
すなわち、
任意の正の数 $\epsilon$ に対して、
\begin{eqnarray}
|x-a| \lt \delta
\hspace{1mm} \Longrightarrow \hspace{1mm}
|f(x) - \alpha | < \epsilon&
\end{eqnarray}
を成り立たせる正の数 $\delta$ が存在する。
$y=f(x)$ とすると、次のように表される。
すなわち、
任意の正の数 $\epsilon$ に対して、
であるとは、次の命題が成り立つことである。
すなわち、
任意の正の数 $\epsilon$ に対して、
\begin{eqnarray}
|x-a| \lt \delta
\hspace{1mm} \Longrightarrow \hspace{1mm}
|f(x) - \alpha | < \epsilon&
\end{eqnarray}
を成り立たせる正の数 $\delta$ が存在する。
$y=f(x)$ とすると、次のように表される。
すなわち、
任意の正の数 $\epsilon$ に対して、
 $$
\tag{1}
$$
を成り立たせる正の $\delta$ が存在する。
$$
\tag{1}
$$
を成り立たせる正の $\delta$ が存在する。
さて、
 も同様に次のように表される。
すなわち、
任意の正の数 $\epsilon'$ に対して、
も同様に次のように表される。
すなわち、
任意の正の数 $\epsilon'$ に対して、
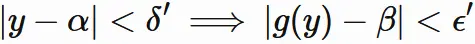 $$
\tag{2}
$$
を成り立たせる正の数 $\delta'$ が存在する。
ここで
$(1)$ が任意の正の $\epsilon$ に対して成り立つことから、
$(1)$ は
$
\epsilon \lt \delta'
$
を満たす $\epsilon$ に対しても成り立つ。
すなわち、
$
\epsilon \lt \delta'
$
を満たす正の数 $\epsilon$ に対して
$$
\tag{2}
$$
を成り立たせる正の数 $\delta'$ が存在する。
ここで
$(1)$ が任意の正の $\epsilon$ に対して成り立つことから、
$(1)$ は
$
\epsilon \lt \delta'
$
を満たす $\epsilon$ に対しても成り立つ。
すなわち、
$
\epsilon \lt \delta'
$
を満たす正の数 $\epsilon$ に対して
 を成り立たせる正の $\delta$ が存在する。
すると、この $\delta$ と
$(2)$ で与えた $\delta'$ に対して、
を成り立たせる正の $\delta$ が存在する。
すると、この $\delta$ と
$(2)$ で与えた $\delta'$ に対して、
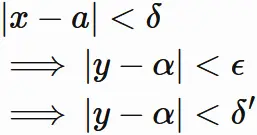 が成り立つ。
これと
$(2)$ から
任意の正の数 $\epsilon'$ に対して、
が成り立つ。
これと
$(2)$ から
任意の正の数 $\epsilon'$ に対して、
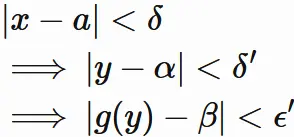 を満たす 正の数 $\delta$
が存在することが示される。
この関係は、
$g(y)=g(f(x)) = h(x)$
を用いると、
次のように表される。
すなわち、
任意の正の数 $\epsilon'$ に対して、
を満たす 正の数 $\delta$
が存在することが示される。
この関係は、
$g(y)=g(f(x)) = h(x)$
を用いると、
次のように表される。
すなわち、
任意の正の数 $\epsilon'$ に対して、
 を満たす 正の数 $\delta$
が存在する。このことは 関数の極限の定義から
を満たす 正の数 $\delta$
が存在する。このことは 関数の極限の定義から
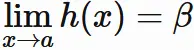 と表される。
と表される。
関数の極限の定義より


さて、