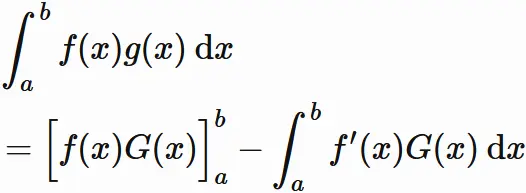部分積分とは?
本ページでは、部分積分の証明を丁寧に行い、
簡単な具体例が添えられています。
| 証明 | |
|---|---|
| - | 部分積分 (不定積分) |
| - | 部分積分 (定積分) |
| 具体例 | |
|---|---|
| - | 例題 |
部分積分 (不定積分)
微分可能な関数 $G(x)$ の微分を $g(x)$ とすると、
$G(x)$ は $g(x)$ の不定積分

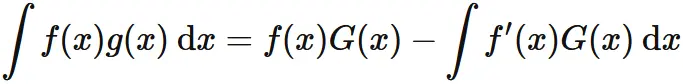
部分積分 (定積分)
微分可能な関数 $G(x)$ の微分を $g(x)$ とすると、
$G(x)$ は $g(x)$ の不定積分
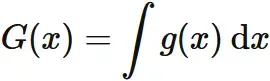
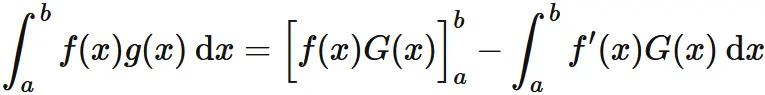
証明
$f(x)g(x)$ の不定積分を $I(x)$ とする。
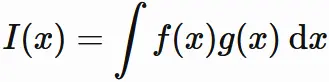 また、$f'(x)G(x)$ の不定積分を $J(x)$ とする。
また、$f'(x)G(x)$ の不定積分を $J(x)$ とする。
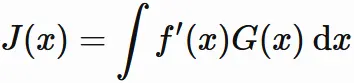 $$
\tag{1}
$$
$I(x)$ は不定積分の部分積分と $(1)$ より、
$$
\tag{1}
$$
$I(x)$ は不定積分の部分積分と $(1)$ より、
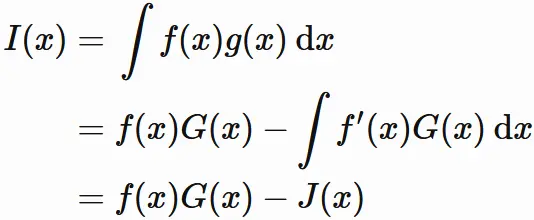 と表せる。
これと定積分の不定積分による表現から
と表せる。
これと定積分の不定積分による表現から
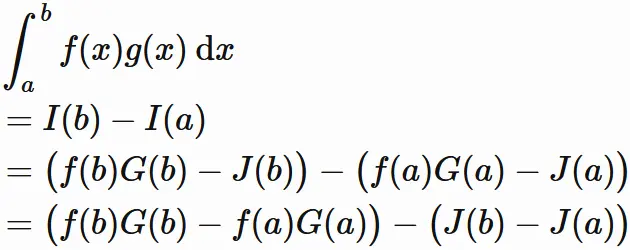 ここで
ここで
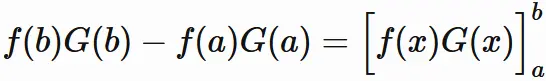 と表すことにすると、
と表すことにすると、
 であるが、$(1)$
と定積分の不定積分による表現から
であるが、$(1)$
と定積分の不定積分による表現から
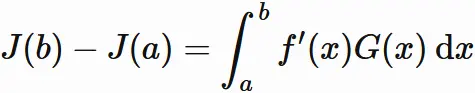 であるので、
であるので、
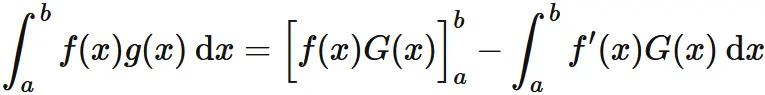 を得る。
を得る。
$f(x)g(x)$ の不定積分を $I(x)$ とする。
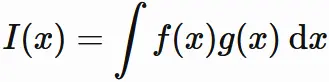
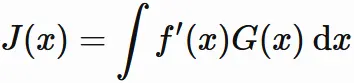
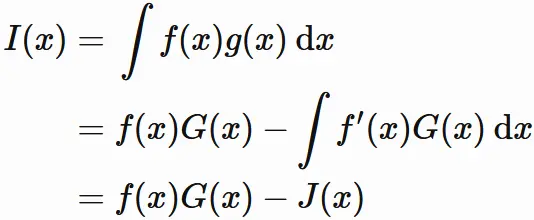
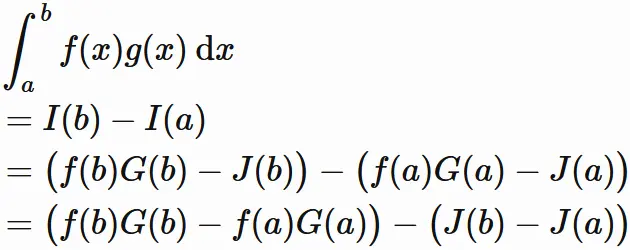
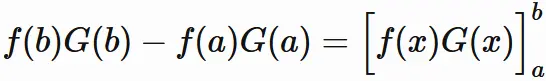

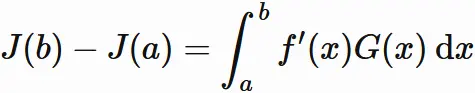
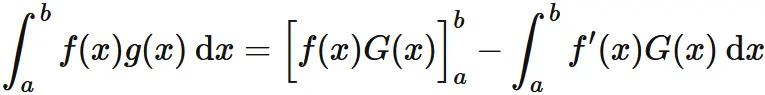
例題
(i) 次の不定積分を部分積分を用いて求めよ。

(ii) 次の定積分を部分積分を用いて求めよ。
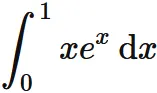
証明
(i)
 とする。
$f(x) = e^{x}$、
$g(x) = \sin x$ として、
部分積分
とする。
$f(x) = e^{x}$、
$g(x) = \sin x$ として、
部分積分
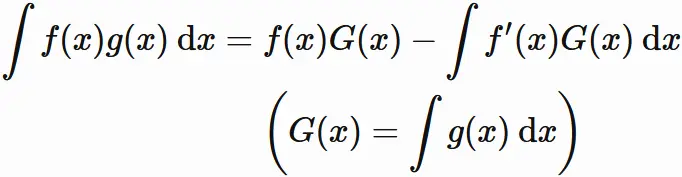 $$
\tag{1}
$$
を適用する。
$$
\tag{1}
$$
を適用する。
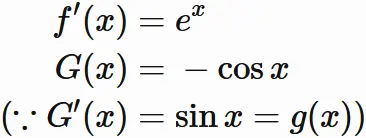 であるので (不定積分の定義を参考)、
であるので (不定積分の定義を参考)、
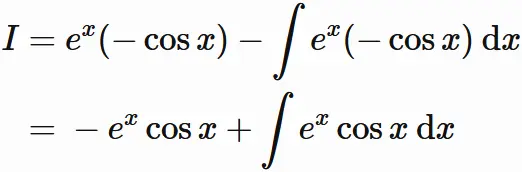 $$
\tag{2}
$$
である。ここで
第二項の積分を
$$
\tag{2}
$$
である。ここで
第二項の積分を
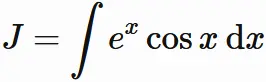 $$
\tag{3}
$$
とし、
$f(x) = e^{x}$、
$g(x) = \cos x$ として、
再び部分積分
$(1)$
を適用すると、
$$
\tag{3}
$$
とし、
$f(x) = e^{x}$、
$g(x) = \cos x$ として、
再び部分積分
$(1)$
を適用すると、
 であるので
であるので
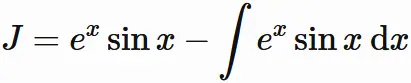 $$
\tag{4}
$$
である。以上 $(2)$ $(3)$ $(4)$ より、
$$
\tag{4}
$$
である。以上 $(2)$ $(3)$ $(4)$ より、
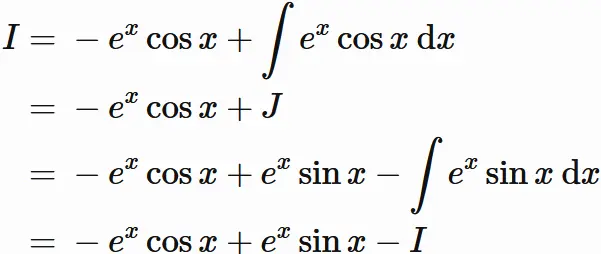 であるので、
であるので、
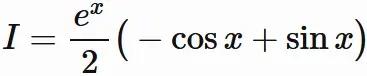 である。
である。
(ii) $f(x) = x$、 $g(x) = e^{x}$ として、 部分積分
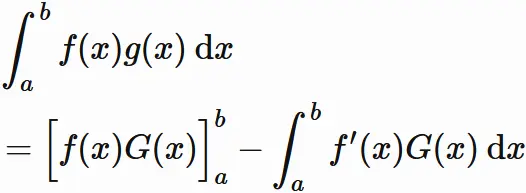 を適用すると、
\begin{eqnarray}
f'(x) &=& 1
\\
G(x) &=& e^{x}
\\
(\because G'(x) &=& e^{x} = g(x))
\end{eqnarray}
を適用すると、
\begin{eqnarray}
f'(x) &=& 1
\\
G(x) &=& e^{x}
\\
(\because G'(x) &=& e^{x} = g(x))
\end{eqnarray}
 であるので
であるので
 である。
である。
(i)

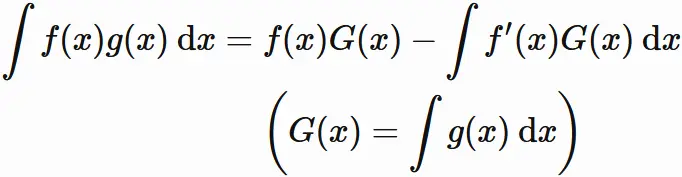
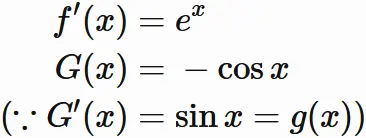
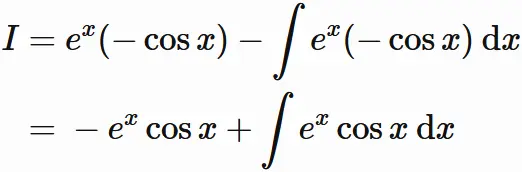
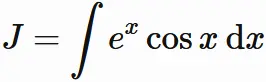

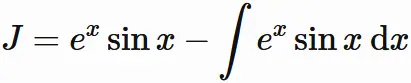
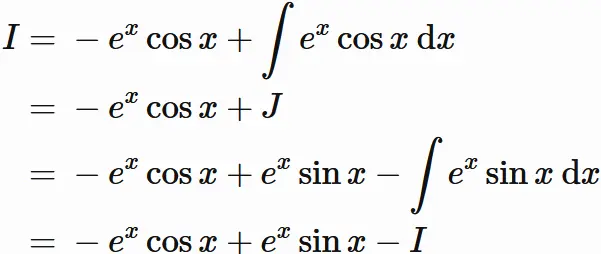
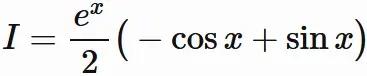
(ii) $f(x) = x$、 $g(x) = e^{x}$ として、 部分積分